APLIKASI GEOMETRI UNTUK PANJANG SEMU BENDA

Penyelidikan ini adalah penyelidikan saya yang pertama selama saya mulai memikirkan tentang pengembangan materi Matemaika.
Dalam inti artikel saya kali ini, saya akan membahas meresensi dari atikel saya yang berjudul “APLIKASI GEOMETRI UNTUK PANJANG SEMU BENDA”, dalam artikel ini saya membahas bagaimana panjang relatif benda yang kita lihat, saya memberi judul semu karena saya menganggap benda yang kita lihat selama ini memiliki panjang semu yang berbeda-beda tergantung dari jarak berapa kita melihatnya, seperti kalau kita melihat sebuah tower dari jarak 10 meter kemudian kita ukur tower tersebut dengan sebuah penggaris yang memiliki jarak tertentu dengan pengamat akan memiliki panjang yang berbeda dengan panjang tower di penggaris pada jarak kita dengan tower yakni 30 meter dan memiliki jarak tertentu dengan pengamat, oleh karena itu dalam artikel ini saya akan memberikan sebuah formula atau rumus yang saya temukan dengan pendekatan geometri.
Pendekatan geometri yang saya maksud ini adalah luas tiga buah bangun ruang , yakni luas segitiga pertama atau kita tulis L, kemudian segitiga kecil atau kita tulis l, dan luas trapesium.
Kita misalkan panjang asli benda adalah Po, kemudian panjang benda dalam penggaris adalah P1, dan jarak antara pengamat dengan benda yang diamati adalah ho, kemudian jarak antara penggaris atau alat pengukur dengan benda adalah h1, dan jarak antara alat pengukur dengan peneliti adalah h2, dari sini kita mendapatkan segitiga ABC atau segitiga besar yang luasnya L dari mata pengamat dengan panjang asli benda (bisa pembaca membayangkan menarik garis dari titik ujung benda ke mata pengamat, begitu juga titik ujung lawannya ditarik sebuah garis tepat ke mata pengamat), selanjutnya hal yang sama dilakukan pada alat ukur, tapi bedanya adalah satu ujung harus pas pada satu garis yang menghubungkan satu titik pada titik benda asli dengan mata pengamat, titik sebaliknya juga harus pas dengan titik di ujung benda asli dengan mata pengamat, dari sini kita mendapatkan segitiga DEB atau segitiga kecil atau dapat ditulis l, kemudian jarak antara benda asli (h1) dengan alat ukur membentuk trapesium ADEC, dari sini kita membuat rumus luas segitiga ABC atau segitiga besar, luas segitiga DEB atau segitiga kecil, dan luas trapesium ADEC. lihat gambar.

perhatikan segitiga ABC yang biasa kita sebut segitiga besar, kemudian segitiga kecil yakni DEB,dan trapesium ADEC.
Luas segitiga ABC atau segitiga besar ( L ) = ½( Po x ho )
Luas segitiga DEB atau segitiga kecil ( l ) = ½( P1 x h2 )
Kemudian luas trapesium ADEC( Lt ) =[ ½( Po + P1 )] x h1
Dari ketiga rumus diatas kita akan mencari panjang benda menurut alat ukur atau P1 atau saya menyebutnya panjang semu benda dengan cara menyamakan laus dari bangun ruang tersebut menjadi:
Luas segitiga ABC ( L )= ( Luas segitiga DEB ( l ) ) + Kemudian luas trapesium ADEC( Lt )
½( Po x ho ) = ½( P1 x h2 ) + [ ½( Po + P1 )] x h1
½( Po x ho ) = ½( P1 x h2 ) + [ ½( Po + P1 )] x h1
½( Po x ho ) = ½[( P1 x h2 ) + ( Po + P1 ) x h1]
Po x ho = P1 x h2 + ( Po + P1 ) x h1
Po x ho = P1 x h2 + (Po x h1+ P1 x h1
Po x ho - Po x h1= P1 x h2 + P1 x h1
Po x ho - Po x h1= P1 x(h2 + h1)
P1 x(h2 + h1) = Po x ho - Po x h1
P1 = [Po x ho - Po x h1]/ (h2 + h1)
P1 = [ho - h1] Po / (h2 + h1)
P1 = [(ho - h1) / (h2 + h1)] x Po...... h2 + h1 = ho dan ho - h1 = h2
P1 = [(h2/ ho] x Po
Jadi panjang semu benda adalah P1 = [(h2/ ho] x Po, dengan :
P1 = Panjang benda menurut alat ukur atau panjang semu benda
h2 = Jarak antara mata pengamat dengan alat ukur atau penggaris
ho = Jarak benda yang diamati dengan mata pengamat
Po = Panjang asli benda
Menurut saya (penulis) rumus ini berlaku juga dengan mengukur kecepatan, suhu, dan radiasi semu benda.

kemiringan

KEMIRINGAN DUA GARIS MEMOTONG DUA SUMBU
Kemiringan Suatu Garis Lurus
Kemiringan suatu garis didefinisikan sebagai sudut antara garis tersebut dengan sumbu x, kemiringan diukur berlawanan dengan arah jarum jam dari arah positif sumbu x ke garis tersebut sehingga sudut kemiringan selalu berada antara 0˚ sampai 180˚. Suatu garis yang sejajar sumbu x, sudut kemiringan α sama dengan 0˚.
Kemiringan (slope) suatu garis adalah tangens dari sudut kemancengannya dan bisa dinyatan dengan m. Definisi kemiringan suatu garis adalah sama dengan definisi kemiringan tangens sudutnya. Tangens α yang biasa ditulis dengan tg α didefinisikan dengan dimana AC dan CB adalah jarak langsung (lihat gambar 1.a)
Sama halnya, apabila (x1,y1) dan (x2,y2) adalah dua titik yang terletak pada suatu garis lurus, maka kemiringan garis tersebut adalah :

harus dicatat bahwa dari suatu sigi tiga yang sama,kemiringan dapat ditentukan secara bebas dengan menentukan dua garis tersebut.lihat gambar 1.b.
Kemiringan garis dapat dikatakan meningkat kekanan apabila x dan y mempunyai tanda yang sama ,serta tg α =Δy/Δx>0 ,dalam kasus ini 0˚˂α˂90˚.
Kemiringan garis kekiri apabila x dan y mempunyai tanda yang berbeda,dan tg α =Δy/Δx .dalam kasus ini nilai α dari 90˚ sampai 180˚

gambar 1.a

gambar 1.b
 
Kemiringan Berpotongan pada Satu Sumbu.
Andaikan diberikan kemiringan m untuk suata garis dan b berpotongan sumbu y di (0,b).seperti gambar 2 dengan memilih (0,b) sebagai (x1,y1) dan menerapkan bentuk kemiringan titik diperoleh
y-b = m(x-0)

yang dapat ditulis ukuran sebagai
y = mx+b

gambar 2
Kemiringan Berpotongan pada Dua Sumbu.
Cara ini akan lebih mudah dan disini kita hanya mencari perpotongan garis lurus pada sumbu xdan sumbu y, dengan ini kita telah memperoleh titik (x1,y1) dan titik (x2,y2), pada titik (x1,y1) kita akan memisalkan y1=0 dan kita akan memperoleh titik (x1,0) pada sumbu x, selanjtnya pada titik (x2,y2) kita misalkan x2=0 sehingga diperoleh titik (0,y2).lihat gambar 3

Gambar 3
Dari titik-titik ini kita akan memasukkannya ke dalam rumus terdahulu,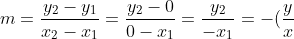
jadi kemiringan garis (m) adalah , perhatikan bahwa fungsi f(x) kita samakan dengan y,oleh karenanya kita akan mendapat nilai f(x) pada fungsi linier f(x) apabila kita memasukkan nilai x=0, dan kita akan mendapat nilai berpotongan pada sumbu x atau kita akan mendapat nilai x apabila kita beri nilai f(x)=0. Jadi dapat disimpulkan dengan sedikit rumus fungsi untuk kemiringan (m) yakni :

Kesimpulan
Kemiringan (slope) atau biasa di simbolkan dengan m adalah sutau garis yang didefinisikan dengan sudut antara garis tersebut dengan sumbu x tidak hanya bisa diukur dengan maupun dengan metode kemiringan berpotongan denga satu sumbu yang mengatakan bahwa nilai kemiringan itu dapat diambil dari nilai atau konstanta yang mengalikan sumbu x pada fungsi yang ditentukan, tapi ada satu metode yang di ajukan oleh penulis yakni metode yang berpotongan pada dua sumbu, dengan formula yang telah diberikan, yakni :

tanda minus yang ada pada rumus diatas adalah sebagai implikasi dari diambilnya sample pada garis yang condong ke kiri, tapi meskipun sample garis diambil mengnghadap ke kanan dan pada waktu mencari nilai kemiringannya hasilnyapun akan sama.




MAKRIPUDIN

perkenalan

kenalkan nama aku makripudin
jenis kelamin laki-laki
aku seorang muslim
aku sekarang masih kuliah di sebuah universitas negeri di Mataram dan sekarang masih menjalani semester IV
umurku sekarang 21 jalan
tujuanku membuat blog adalah supaya aku bisa menyalurkan tulisan-tulisan yang pernah aku buat dan mudah-mudahan bisa bermamfaat bagi ilmu pengetahuan yang terus berkembang sampai saat ini
cita-citaku menjadi seorang matematikawan
aku berasal dari laombok timur, NTB, indonesia
blog yang sepadan dengan ini adalah di makripudin.blogspot.com